整体模块功能图

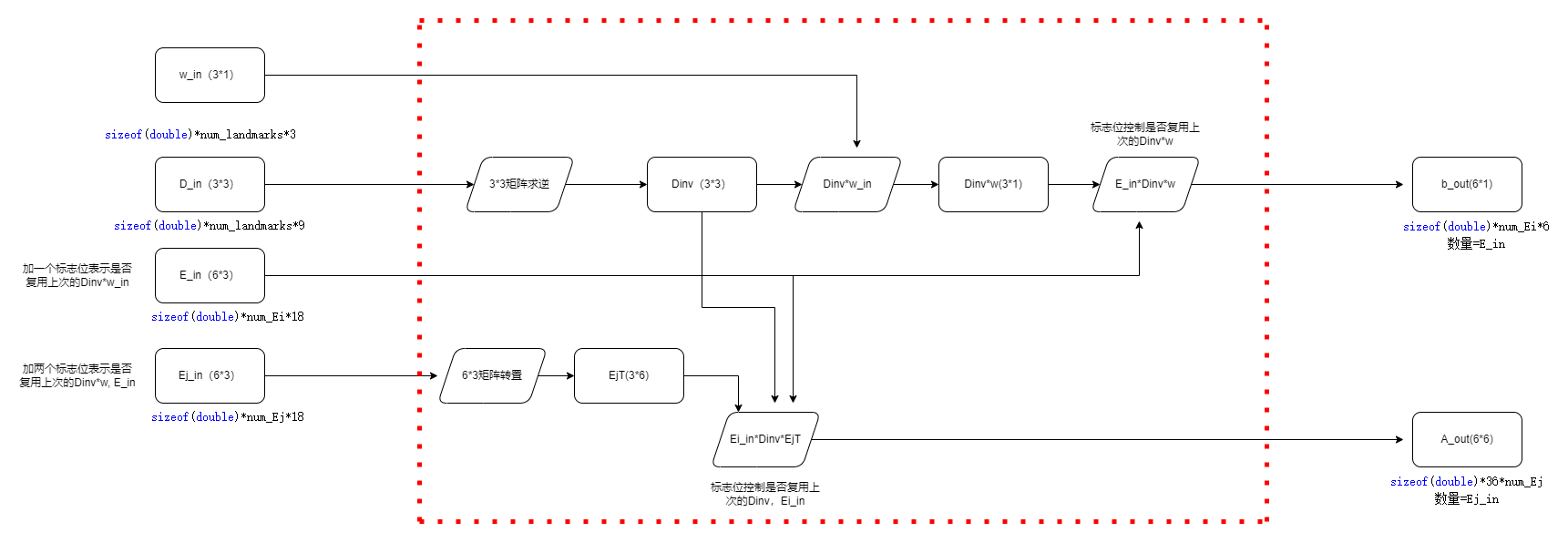
BA_module

这里主要涉及到矩阵求逆、矩阵转置和矩阵乘法的操作，最后输出结果的矩阵。

矩阵求逆

矩阵求逆主要有两种方法，一种是利用伴随阵求逆矩阵的方法，还有其他方法是利用矩阵的L-U分解法等（L-U分解法具有更加广泛的应用范围，其可以并行计算）

L-U分解法
$$
A = LU \
A^{-1} = U^{-1}L^{-1}
$$
其中，L是下三角阵，U是上三角阵。
$$
\begin{bmatrix}
A_{11} & A_{12} \
A_{21} & A_{22}
\end{bmatrix}

\begin{bmatrix}
L_{11} & \
L_{21} & L_{22}
\end{bmatrix}
\times
\begin{bmatrix}
U_{11} & U_{12} \
& U_{22}
\end{bmatrix}
$$

$$
\left{
\begin{array}{lr}
A_{11} = L_{11}U_{11} \
A_{12} = L_{11}U_{12} \
A_{21} = L_{21}U_{11} \
A_{22} = L_{21}U_{12} + L_{22}U_{22}
\end{array}
\right.
$$

上式表明，其可以作并行计算

FIFO

求FIFO深度需要考虑最坏的情形，读写的速率应该相差最大，也就是说需要找出最大的写速率和最小的读速率；不管什么场景，要确定FIFO的深度，关键在于计算出在突发读写这段时间内有多少个数据没有被读走。

最坏情况：

给定数据传输的速率，不给数据传输的方式，考虑最坏情况是下图的case-4（背靠背），连续读取了最多的数据，需要的FIFO是最大的。

img

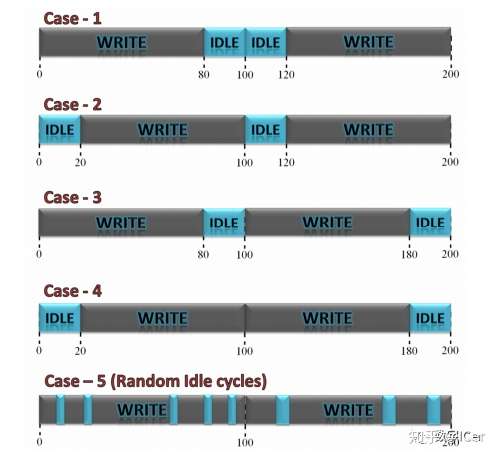
推导公式：

  • 写时钟周期为clkw
  • 读时钟周期为clkr
  • 在读时钟周期内，每x个周期内可以有y个数据读出FIFO，即读数据的读数率
  • 在写时钟周期内，每m个周期内就有n个数据写入FIFO
  • 背靠背“的情形下是FIFO读写的最坏情形，burst长度 B = 2*n

FIFO最小深度为：
$$
depth = 2n - 2m\times\frac{y}{x} = B - B\times\frac{clkr}{clkw}\times\frac{y}{x}
$$

总结

要计算这里的FIFO深度的最坏情况，也就是要计算写操作burst的最大长度（当给定数据传输速率后，选择背靠背的传输方式为最大）。

参考资料

  1. FIFO深度计算 - 知乎 (zhihu.com)